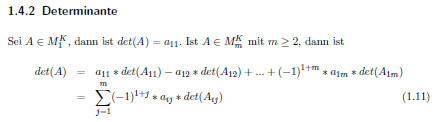
Zur Vorbereitung auf die Mathematikprüfung für die Zulassung zum Informatikstudium habe ich mir auf 73 Seiten eine Formelsammlung zusammengestellt, die die wichtigsten Gebiete abdeckt. Zu jedem Thema gibt es auch durchgerechnete Beispielaufgaben mit Anmerkungen, damit die richtige Anwendung klar ist.

Ich hoffe, dass sie auch anderen Hilfreich sein kann. Für einen Überblick hier das Inhaltsverzeichnis:

1 Lineare Algebra                                              1

1.1 Vektorräume . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  1
1.1.1 Abelsche Gruppe (1 Operation - + oder *) . . . . . . . . . . . . 1
1.1.2 Körper ( 2 Operationen - + und *) . . . . . . . . . . . . . . . . . . 1
1.1.3 Vektorraum V über K . . . . . . . . . . . . . . . . . . . . . . . . . . .  2
1.1.4 Linearkombination . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  5
1.1.5 Linear unabhängig . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.1.6 Dimension von V . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.1.7 Homomorphismus (lineare Abbildung) . . . . . . . . . . . . . . . . .14
1.1.8 Bilinearform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
1.1.9 Skalarprodukt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1.1.10 Orthogonal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1.1.11 Orthogonalraum . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1.2 Lineare Gleichungssysteme (LGS) . . . . . . . . . . . . . . . . . . .  20
1.2.1 Matrizenprodukt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
1.2.2 Lösungsmenge eines LGS . . . . . . . . . . . . . . . . . . . . . . . .  21
1.2.3 Transformationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
1.2.4 Gauss-Jordan-Verfahren . . . . . . . . . . . . . . . . . . . . . . . .  22
1.3 Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .   24
1.3.1 Typen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
1.3.2 Matrizen Transposition . . . . . . . . . . . . . . . . . . . . . . . . . . 26
1.3.3 Matrizen Addition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
1.3.4 Matrizenmultiplikation . . . . . . . . . . . . . . . . . . . . . . . . . .  26
1.3.5 Rang einer Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
1.3.6 Matrizentransformationen . . . . . . . . . . . . . . . . . . . . . . . .  27
1.4 Determinanten und invertierbare Matrizen . . . . . . . . . . . . .  28
1.4.1 Matrix Aij . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  28
1.4.2 Determinante . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
1.4.3 Reguläre Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  30
1.4.4 Matrixgleichung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  30
1.4.5 Inverse Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  32

2 Graphentheorie                                                   34

2.1 Graphen Grundlagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
2.1.1 Graph . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
2.1.2 Schlinge . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  34
2.1.3 Schlichter Graph . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  34
2.1.4 Grad eines Knoten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
2.1.5 Handschlaglemma . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  35
2.1.6 Vollständiger Graph . . . . . . . . . . . . . . . . . . . . . . . . . . . .  35
2.1.7 Komplementgraph . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  36
2.1.8 Untergraph . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
2.1.9 Kantenzug . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  37
2.1.10 Zusammenhängender Graph . . . . . . . . . . . . . . . . . . . . . .  37
2.1.11 Isomorphe Graphen . . . . . . . . . . . . . . . . . . . . . . . . . . . .  37
2.1.12 Wald . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  38
2.1.13 Baum . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
2.2 Gerichtete Graphen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
2.2.1 Gerichteter Graph . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
2.2.2 Grad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
2.2.3 Gerichteter Kantenzug . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
2.2.4 Starker Zusammenhang . . . . . . . . . . . . . . . . . . . . . . . . . . 39
2.2.5 Azyklischer Graph . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
2.3 Darstellung von Graphen im Computer . . . . . . . . . . . . . . . . . . 40
2.3.1 Adjazenzmatrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  40
2.3.2 Adjazenzliste . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
2.4 Durchsuchen von Graphen . . . . . . . . . . . . . . . . . . . . . . . . . .  42
2.4.1 Tiefensuche . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
2.4.2 Artikulationspunkt . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  42
2.4.3 Breitensuche . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
2.4.4 Topologisches Sortieren . . . . . . . . . . . . . . . . . . . . . . . . . . 44
2.5 Kreis und Wegeprobleme . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
2.5.1 Eulersche Kreise . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  45
2.5.2 Algorithmus von Hierholzer . . . . . . . . . . . . . . . . . . . . . . .  46
2.5.3 Hamiltonsche Kreise . . . . . . . . . . . . . . . . . . . . . . . . . . . .  46
2.6 Kürzeste Wege . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .   47
2.6.1 Kantengewicht . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .   47
2.6.2 Abstand . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  47
2.6.3 Algorithmus von D¼kstra . . . . . . . . . . . . . . . . . . . . . . . .   48
2.7 Aufspannende Bäume . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  51
2.7.1 Aufspannender Baum . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
2.7.2 Minimal aufspannender Baum . . . . . . . . . . . . . . . . . . . . . .  51
2.7.3 Abzählung von aufspannenden Bäumen . . . . . . . . . . . . . . .  52
2.7.4 Prüfercode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
2.7.5 Algorithmus von Prim . . . . . . . . . . . . . . . . . . . . . . . . . . .  54
2.7.6 Algorithmus von Kruskal . . . . . . . . . . . . . . . . . . . . . . . . .  55
2.7.7 Traveling Salesman Problem (TSP) . . . . . . . . . . . . . . . . . .  56

3 Wahrscheinlichkeit                                              57

3.1 Der Wahrscheinlichkeitsraum . . . . . . . . . . . . . . . . . . . . . .  57
3.1.1 Ereignisfeld I . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
3.1.2 Vollständiges Ereignissystem . . . . . . . . . . . . . . . . . . . . .   58
3.1.3 Eigenschaften der relativen Häufigkeit . . . . . . . . . . . . . . .  58
3.1.4 Eigenschaften der Wahrscheinlichkeit . . . . . . . . . . . . . . . . 58
3.1.5 De Morgansche Regeln . . . . . . . . . . . . . . . . . . . . . . . . . .  59
3.1.6 Kombinatorische Formeln . . . . . . . . . . . . . . . . . . . . . . . .  59
3.2 Der klassische Wahrscheinlichkeitsbegriff . . . . . . . . . . . . .  59
3.2.1 Laplace Versuch . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  59
3.2.2 Bedingte Wahrscheinlichkeit . . . . . . . . . . . . . . . . . . . . . . . 60
3.2.3 Produktformel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  60
3.2.4 Stochastisch unabhängig . . . . . . . . . . . . . . . . . . . . . . . . . 60
3.2.5 Produktformel für bedingte Wahrscheinlichkeit . . . . . . . . . .   61
3.3 Totale Wahrscheinlichkeit und Bayes’sche Formel . . . . . . .  62
3.3.1 Totale Wahrscheinlichkeit . . . . . . . . . . . . . . . . . . . . . . . .  62
3.3.2 Formel von Bayes . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  63
3.4 Diskrete Zufallsgrößen . . . . . . . . . . . . . . . . . . . . . . . . . . . .   64
3.4.1 Gleichverteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
3.4.2 Binomialverteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
3.4.3 Poissonverteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  66
3.5 Stetige Zufallsgrößen . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  67
3.5.1 Dichtefunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  67
3.5.2 Verteilungsfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . .  67
3.5.3 Bedingte Wahrscheinlichkeiten . . . . . . . . . . . . . . . . . . . . . 67
3.5.4 Gleichverteilung auf [a,b] . . . . . . . . . . . . . . . . . . . . . . . . 68
3.5.5 Dreiecksverteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  68
3.5.6 Exponentialverteilung mit Parameter  . . . . . . . . . . . . . . . . . 68
3.5.7 Normalverteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  69
3.5.8 Satz von Moivre und Laplace . . . . . . . . . . . . . . . . . . . . . . 69
3.5.9 Erwartungswert und Varianz . . . . . . . . . . . . . . . . . . . . . . . 70
3.5.10 Ungleichung von Tschebyscheff . . . . . . . . . . . . . . . . . . . 70
3.5.11 Übersichtstabelle Verteilungsfunktionen . . . . . . . . . . . . . . 71

4 Formeln                                                                           72

4.1 Differentialrechnung - Regeln zur Ableitung . . . . . . . . . . . . . . . 72
4.2 Integralrechnung - Stammfunktionen und Regeln . . . . . . . . . . .  73

5 Programme                                                                      74

5.1 Geogebra . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
5.2 Maxima . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  75
5.3 yEd Graph Editor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
5.4 math4u2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  85
5.5 GraphAnalyser . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  86
5.6 Lyx . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  88
5.7 Sonstiges . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  89

6 Literaturverzeichnis                                                           90

Die Formelsammlung kann hier als PDF heruntergelagen werden.