GraphAnalyser

Der GraphAnalyser ist ein kleines Programm, das einen Graphen in Form einer Textdatei entgegen nimmt und ihn auswertet. Das Ergebnis erhält man als Textdatei zurück.
Das Programm habe ich während des Studiums (Mathematik - Graphentheorie) geschrieben. Es erlaubt das Überprüfen von Ergebnissen.

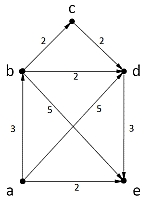Dieser Graph hätte folgende Eingabedatei:  ; Beispiel Eingabedatei Vetrexes = {a,b,c,d,e} Edges = {(a,b,3),(a,d,5),(a,e,2),(b,c,2),(b,d,2),(b,e,5),(c,d,2),(d,e,3)}

Diesen Text speichert man unter einem Namen ab und läßt die Datei anschließend auf das Icon des GraphAnalyser fallen. Als Ergebnis erhält man das folgende Textfile, das automatisch öffnet:

Input Data:

Vetrexes={a,b,c,d,e}
Edges={(a,b,3),(a,d,5),(a,e,2),(b,c,2),(b,d,2),(b,e,5),(c,d,2),(d,e,3)}

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Edges:
       1   2   3   4   5   6   7   8  
       --  --  --  --  --  --  --  --
From: |a | a | a | b | b | b | c | d |
Rate: |3 | 5 | 2 | 2 | 2 | 5 | 2 | 3 |
To  : |b | d | e | c | d | e | d | e |

Graph type: directed
Edges are : rated

Out Degree:
 
[a] =3 | [b] =3 | [c] =1 | [d] =1 | [e] =0 |
 
In Degree:
 
[a] =0 | [b] =1 | [c] =1 | [d] =3 | [e] =3 |
 
Eulerway possible. Start from vertex[a] and end in vertex[e].
 
MinDegree of Graph: 2 in vertex [c]
MaxDegree of Graph: 4 in vertex [b]
 
Adjacencmatrix:

    a b c d e

a | 0 3 0 5 2 |
b | 0 0 2 2 5 |
c | 0 0 0 2 0 |
d | 0 0 0 0 3 |
e | 0 0 0 0 0 |

Adjacenclist:

[a] | -> [b] -> [d] -> [e]
[b] | -> [c] -> [d] -> [e]
[c] | -> [d]
[d] | -> [e]
[e] |

Deep Find Search starting from each vertex:

 | (Part 1) -> [a] -> [b] -> [c] -> [d] -> [e] |
 | (Part 1) -> [b] -> [c] -> [d] -> [e] | (Part 2) -> [a] |
 | (Part 1) -> [c] -> [d] -> [e] | (Part 2) -> [a] -> [b] |
 | (Part 1) -> [d] -> [e] | (Part 2) -> [a] -> [b] -> [c] |
 | (Part 1) -> [e] | (Part 2) -> [a] -> [b] -> [c] -> [d] |

Breadth First Search starting from each vertex:

 | (Part 1) -> [a] -> [b] -> [d] -> [e] -> [c] |
 | (Part 1) -> [b] -> [c] -> [d] -> [e] | (Part 2) -> [a] |
 | (Part 1) -> [c] -> [d] -> [e] | (Part 2) -> [a] -> [b] |
 | (Part 1) -> [d] -> [e] | (Part 2) -> [a] -> [b] -> [c] |
 | (Part 1) -> [e] | (Part 2) -> [a] -> [b] -> [d] -> [c] |

Prim (minimal spanning tree) starting from each vertex:

Starting from [a] : | [a] -2> [e] | [a] -3> [b] | [b] -2> [c] | [b] -2> [d] | Sum = 9
Starting from [b] : | [b] -2> [c] | [b] -2> [d] | [d] -3> [e] | Break! Only 4 of 5 vertexes in minimal spanning tree. => [a], are out of tree. | Sum = 7
Starting from [c] : | [c] -2> [d] | [d] -3> [e] | Break! Only 3 of 5 vertexes in minimal spanning tree. => [a],[b], are out of tree. | Sum = 5
Starting from [d] : | [d] -3> [e] | Break! Only 2 of 5 vertexes in minimal spanning tree. => [a],[b],[c], are out of tree. | Sum = 3
Starting from [e] : | Break! Only 1 of 5 vertexes in minimal spanning tree. => [a],[b],[c],[d], are out of tree. | Sum = 0

Dijkstra (shortest way) starting from each vertex:

Start from [a] | [a] -0-> [a] | [a] -3-> [b] | [b] -2-> [c] | [a] -5-> [d] | [a] -2-> [e] |
Waylength : a = 0 | b = 3 | c = 5 | d = 5 | e = 2 |
Way from [a] to [e] : [a] -2-> [e] = 2
Way from [a] to [d] : [a] -5-> [d] = 5
Way from [a] to [c] : [a] -3-> [b] -2-> [c] = 5
Way from [a] to [b] : [a] -3-> [b] = 3

Start from [b] | [a] -0-> [a] | [b] -0-> [b] | [b] -2-> [c] | [b] -2-> [d] | [b] -5-> [e] |
Waylength : a = max | b = 0 | c = 2 | d = 2 | e = 5 |
Way from [b] to [e] : [b] -5-> [e] = 5
Way from [b] to [d] : [b] -2-> [d] = 2
Way from [b] to [c] : [b] -2-> [c] = 2

Start from [c] | [a] -0-> [a] | [b] -0-> [b] | [c] -0-> [c] | [c] -2-> [d] | [d] -3-> [e] |
Waylength : a = max | b = max | c = 0 | d = 2 | e = 5 |
Way from [c] to [e] : [c] -2-> [d] -3-> [e] = 5
Way from [c] to [d] : [c] -2-> [d] = 2

Start from [d] | [a] -0-> [a] | [b] -0-> [b] | [c] -0-> [c] | [d] -0-> [d] | [d] -3-> [e] |
Waylength : a = max | b = max | c = max | d = 0 | e = 3 |
Way from [d] to [e] : [d] -3-> [e] = 3

Start from [e] | [a] -0-> [a] | [b] -0-> [b] | [c] -0-> [c] | [d] -0-> [d] | [e] -0-> [e] |
Waylength : a = max | b = max | c = max | d = max | e = 0 |

Matrix ^1:

    a b c d e

a | 0 1 0 1 1 |
b | 0 0 1 1 1 |
c | 0 0 0 1 0 |
d | 0 0 0 0 1 |
e | 0 0 0 0 0 |

Matrix ^2:

    a b c d e

a | 0 0 1 1 2 |
b | 0 0 0 1 1 |
c | 0 0 0 0 1 |
d | 0 0 0 0 0 |
e | 0 0 0 0 0 |

Matrix ^3:

    a b c d e

a | 0 0 0 1 1 |
b | 0 0 0 0 1 |
c | 0 0 0 0 0 |
d | 0 0 0 0 0 |
e | 0 0 0 0 0 |

Matrix ^4:

    a b c d e

a | 0 0 0 0 1 |
b | 0 0 0 0 0 |
c | 0 0 0 0 0 |
d | 0 0 0 0 0 |
e | 0 0 0 0 0 |

Matrix ^5: Finished - all Zero!

--- Break on raising matrix ---

Das Programm das auch viele Beispiele enthält kann am ende des englischen Textes heruntergeladen werden.

Da das Programm sicher auch nicht deutschsprachige Studenten interessieren könnte, kommt hier das englische ReadMe:

GraphAnalyser
-------------

This program makes some simple analyses out of a given List of vetexes and edges and helps validating own results by learning the first steps of graph theory.

Using the program is quite simple. Write a vertex and edge list in a simple textfile. Then drop the textfile on the GraphAnalyser icon or double-click the icon and choose the textfile in the opening file dialog box.

Now GraphAnalyser will calculate some things and write them in a textfile named like the input file with an extension ("filename_result.txt"). Then Notepad will open and shows the resultfile.

The input file is written by following syntax:

- Lines beginning with ";" are remark lines and will be ignored
- Lines beginning with "Vertexes=" are parsed to get the vertexes
- Lines beginning with "Edges=" are parsed to get the edges.

If you are using curly brackets, the edges information is interpreted as not directed.
If you are using round brackets, the edges information is interpreted as directed.
If you use a 3rd parameter in the brackets this is used to make the edges rated. You have to use the 3rd parameter in all or in none edge definition. Don't mix it!

Vertex names have to start with a letter - not with a number! If your sample uses numbers as vertex names then prefix a letter like "v". Is your vertex list greater than 9 please use a leading zero for numbers less 10 - otherwise "v4" will be sorted after "v10" because of the string compare.

Here are some sample input definitions:

; Sample 1 - five vertexes and seven directed and rated edges
Vetrexes = {a,b,c,d,e}
Edges = {(a,b,33),(a,d,55),(a,e,22),(b,c,22),(b,d,22),(b,e,55),(c,d,22)}

; Sample 2 - five vertexes and eight undirected and unrated edges
Vetrexes = {a,b,c,d,e}
Edges = {{a,b},{a,d},{a,e},{b,c},{b,d},{b,e},{c,d},{d,e}}

The program is written in AutoIt (www.autoitscript.com). As i'm a system administrator it's the tool i'm working with every day and i don't have to think about most of the things i want to implement. So i choose this programming language.

The program is not optimised for speed neither for memory usage. I use a adjacencematrix to implement the logic and determine the results.

Please feel free to contact me by e-mail. It would be nice if you report any errors to me.